Como usar o “Solver” para resolver problemas de otimização em sua empresa
Atualizado em 11/05/22 - Escrito por Celso Monteiro na(s) categoria(s): Custos e Finanças / Engenharia de produto / Estratégia / Processos e Organização
A primeira (e inevitável) pergunta que farei nesse artigo é: você conhece a ferramenta “Solver” disponível no Excel? Caso positivo, é muito provável que tenha visto como usar o solver em algum curso de engenharia ou administração, já que a prática é muito utilizada em cadeiras ofertadas por esses cursos. Caso soe estranho aos seus ouvidos, prepare-se, pois ela pode mudar o futuro da sua empresa.
No momento atual do país, tudo o que o gestor de empresa busca é otimizar os resultados de seu empreendimento, maximizar lucro, minimizar despesas, potencializar a capacidade utilizada das máquinas, dentre outros objetivos. É muito difícil tomar decisões sem informações que comprovem a assertividade da mesma, principalmente se levarmos em consideração o leque de restrições que devem ser consideradas.

Imagine uma empresa que fabrique 5 produtos diferentes, todos com custos de fabricação, preços de venda e tempos de fabricação distintos entre si. O gestor da empresa busca otimizar seu lucro e deseja saber a quantidade a ser produzida, por mês, de cada um dos 5 produtos. Seria muito fácil tomar essa decisão se analisássemos apenas o lucro. Neste caso, pegaríamos o preço de venda e diminuiríamos o seu custo de produção para saber o ganho. Se o “Produto A” é o mais rentável, é muito cômodo pensar que para otimizar seu lucro, basta produzir somente este item e “esquecer os demais”.
Não é assim que a “banda toca”, meu amigo. Existe uma série de restrições que impedem você de fazer essa sandice, como a manutenção do mix de produtos, tempo disponível de cada máquina, recursos financeiros escassos para produzir grandes quantidades, aceitação do mercado, etc. Logo, a equação a ser feita para tomar a simples decisão do quanto produzir já toma ares de dramaticidade.
Calma, não precisa perder o seu sono…. Com uma boa dose de compreensão da sua necessidade mais alguns conceitos da ferramenta Solver, você conseguirá sair dessa situação e enxergar uma resposta de forma rápida.
Neste artigo darei alguns conceitos básicos de programação Linear que servirão como base para a inserção dos dados no Solver (EXCEL) de forma correta. O objetivo é que você saiba como usar o solver na prática.
Como eu consigo entender muito mais rápido um assunto quando o conteúdo é apresentado em forma de exemplos e não de teoria pura, para lhes explicar os conceitos básicos de Programação Linear, utilizarei um exemplo e explicarei cada etapa do mesmo para facilitar a compreensão do conteúdo deste artigo.
O CASO DA FÁBRICA DE BRINQUEDOS QUE QUERIA MAXIMIZAR SEUS LUCROS
A Fábrica Diversão S.A. produz brinquedos de madeira e possui dois itens em seu mix de produção: trem e avião. Para fabricar o trem a empresa utiliza R$ 9,00/und de matéria prima, dispõe de custos de mão de obra e indiretos de fabricação na ordem de R$ 10,00/und. Já o avião utiliza R$ 10,00/und de matéria prima, dispõe de R$14/und para mão de obra direta e custos indiretos de fabricação. O trem é vendido a R$ 21,00 e o avião é vendido a R$ 27,00. Cada unidade de trem demanda de 1 hora de carpintaria e 1 hora de pintura, já o avião demanda 1 hora de carpintaria e 2 horas de pintura.
A empresa gostaria de saber a quantidade a ser produzida de cada um desses itens, semanalmente, levando em consideração as seguintes restrições:
– Disponibilidade da carpintaria de até 80h / semana
– Disponibilidade da pintura de até 100h / semana
– Não produzir mais do que 40 aviões, pois essa é a demanda máxima do produto por semana
Definindo as variáveis
As variáveis são os resultados que deseja obter, neste caso da Diversão S.A., a empresa deseja saber a quantidade a ser produzida semanalmente para otimizar seus lucros. Portanto, as variáveis dessa equação são:
– X1 = Qtd a produzir de trem / semana
– X2 = Qtd a produzir de avião / semana
Definindo a função objetivo
A função objetivo necessita conter uma otimização, ou seja, precisa buscar aprimorar ou minimizar alguma função matemática. No nosso exemplo, a função objetivo é maximizar o ganho com a venda de seus produtos. Como o lucro é calculado (de forma simples) pela diferença entre o preço de venda e os custos de fabricação, temos que o lucro de cada um dos produtos é:
– TREM = R$21 – R$9 – R$10 = R$2 / UND
– AVIÃO = 27 – R$10 – R$14 = R$3 / UND
Logo, a função objetivo da Diversão S.A. será :
Max(lucro) = 2*X1 + 3*X2
Definindo as restrições
As restrições servem para que consigamos incluir na função objetivo um conjunto de regras, que precisam ser respeitadas, de forma que o resultado apresentado seja o mais condizente possível com a realidade da empresa ou do mercado.
No nosso exemplo, temos 5 restrições:
CARPINTARIA
Cada um dos produtos precisa executar atividades no setor de carpintaria, porém, semanalmente, este setor dispõe de uma capacidade limitada de horas para serem utilizadas em produção (80 horas). Logo, a restrição da carpintaria é descrita pela fórmula:
1*X1 + 1*X2 <= 80
PINTURA
Cada um dos produtos também precisa executar atividades no setor de pintura, que por sua vez dispõe de 100 horas semanais para atividades de produção . Logo, a fórmula da restrição seria:
1*X1 + 2*X2 <= 100
DEMANDA DE AVIÃO
No exemplo também foi identificado que a produção de avião não pode exceder 40 unidades, já que essa é a demanda máxima de avião por semana. A fórmula da restrição seria:
X2 <= 40
NÃO NEGATIVIDADE
Essa é uma restrição comum nos problemas de programação linear e que utilizam o Solver. A não negatividade representa que os resultados obtidos para cada uma deve ser maior ou igual a zero. Nenhum resultado deve ser calculado com valores negativos. A restrição é descrita pela seguinte fórmula:
X1 >= 0
X2 >= 0
Em resumo, todo o texto e aqueles dados contidos no texto da Diversão S.A. podem ser descritos , simplesmente, por:
– X1 = Qtd a produzir de trem / semana
– X2 = Qtd a produzir de avião / semana
OBJETIVO -> Max(lucro) = 2*X1 + 3*X2
RESTRIÇÕES -> 1*X1 + 1*X2 <= 80
1*X1 + 2*X2 <= 100
X2 <= 40
X1 >= 0
X2 >= 0
Como usar o solver na prática
Como eu utilizo o Excel 2007, os passos que darei no artigo são exclusivos para essa versão , porém, para aqueles que possuem versões diferentes basta acessar o Youtube e buscar por “tutorial para habilitar o solver no Excel XXXX (Ano da sua versão)”. Esse passo é fundamental para continuar a descobrir como usar o solver.
O primeiro passo é clicar em no botão “Iniciar” e clicar sobre o botão “Opções do Excel”.
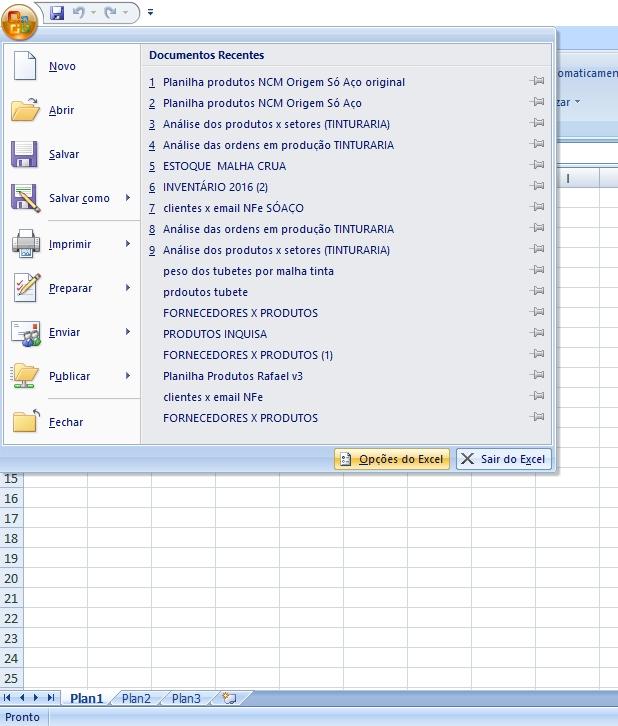
Agora, vá em Suplementos e clique no botão Ir… ao lado direito de Gerenciar.
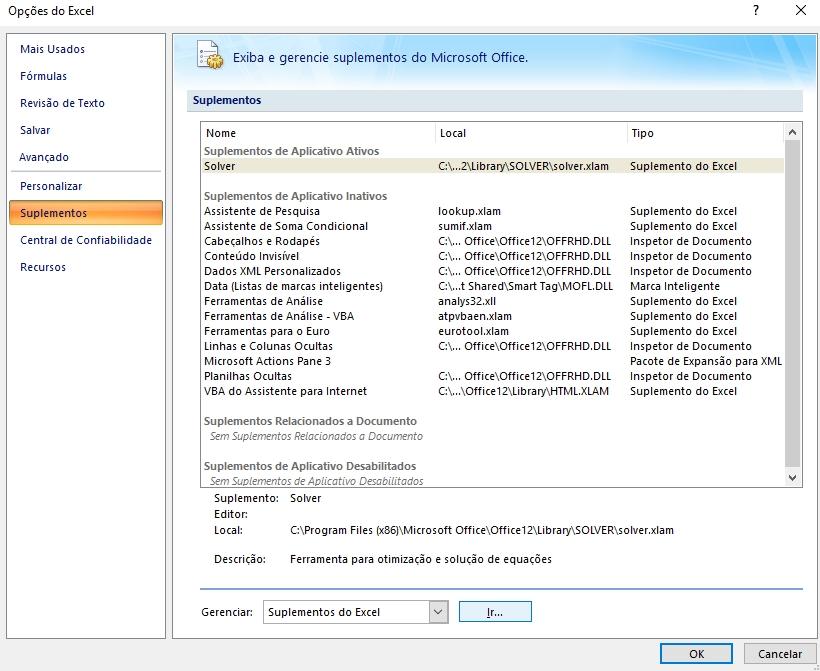
Após o Excel carregar todos os suplementos da sua versão, clique na caixinha ao lado do suplemento Solver e clique em OK.
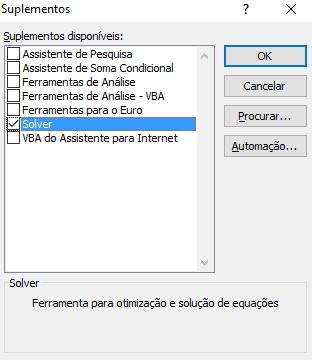
Pronto, agora o seu Excel irá instalar o suplemento e você poderá utilizá-lo para resolver seus problemas de programação linear.
Com o Solver instalado, vamos iniciar a inclusão dos parâmetros da nossa representação matemática no Excel. Assim como identificado no artigo anterior, sugiro seguirmos a mesma ordem para a parametrização do problema no Excel: Identificar variáveis, função objetivo, restrições.
Variáveis do problema
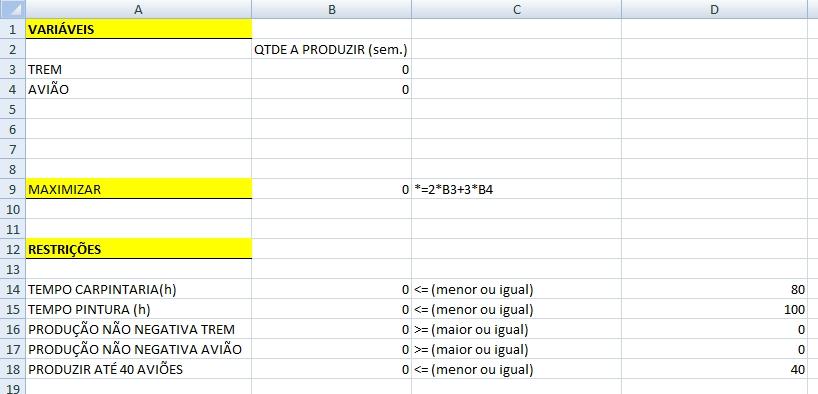
Temos duas variáveis no nosso exemplo X1 (quantidade a produzir de trem/semana) e X2 (quantidade a produzir de avião/semana). Vamos informar essas variáveis da seguinte maneira:
Criamos duas linhas, uma para o trem e outra para o avião, e ao lado de cada um deles informar o valor igual a zero.
Função objetivo
A função objetivo será uma representação do lucro de cada um dos produtos , caso a produção seja vendida. Logo, a mesma será representada da seguinte forma:
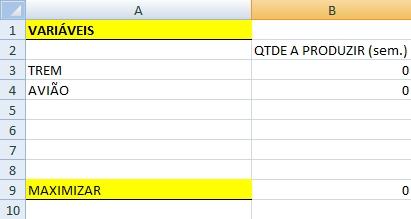
Na célula B9, referente a função objetivo, eu passei o seguinte valor:
=2*B3+3*B4
Onde B3 é a célula referente a quantidade de trem e B4 é a célula para a quantidade de aviões.
Restrições
Para não confundir uma restrição com a outra, sugiro criá-las em linhas distintas e sempre identificá-las com expressões que possam ser facilmente relacionadas a elas individualmente.
Para facilitar a compreensão, irei informar as fórmulas usadas em cada uma das restrições e configuradas na coluna B.
TEMPO CARPINTARIA(h) = 1*B3+1*B4
TEMPO PINTURA (h) = 1*B3+2*B4
PRODUÇÃO NÃO NEGATIVA TREM = B3
PRODUÇÃO NÃO NEGATIVA AVIÃO = B4
PRODUZIR ATÉ 40 AVIÕES = B4
Na coluna C eu indiquei a condição (se era maior ou menor) apenas para referência e na coluna D eu informei os valores de cada restrição, conforme identificado anteriormente.
Parametrizando o Solver
Agora, com toda a esquematização pronta, você precisará acessar o menu superior do Excel, entrar na aba Dados e selecionar o ícone do Solver, que ficará na parte direita do menu, ao final de todas as opções.

Após o Excel abrir o Solver, ele pedirá para que você informe todos os parâmetros para que ele calcule corretamente o resultado da sua equação.
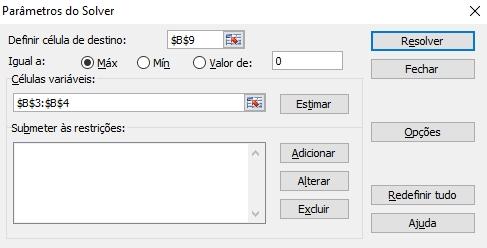
Na linguagem do Solver, a célula de destino é a célula que você definiu a função objetivo, que, no meu caso, é a B9. Basta você clicar na imagem que contém uma pequena tabela, à direita do campo para a definição da célula de destino, e selecionar a célula que está representando a função objetivo na sua planilha. Como a minha é a B9 o Excel representou a mesma como $B$9.
Em igual a, selecionar qual a otimização você quer obter com a função objetivo. Como a Diversão S.A. busca maximizar seu lucro semanal, selecionei a opção Máx.
Na seção Células variáveis clicar no mesmo ícone ao lado direito e selecionar na tabela quais são as células que representarão as variáveis da equação. No meu caso, as variáveis são as células B3 e B4, onde o Solver as representou como $B$3:$B$4.
Na seção Submeter às restrições você irá clicar no botão Adicionar e incluirá todas as restrições, uma a uma.
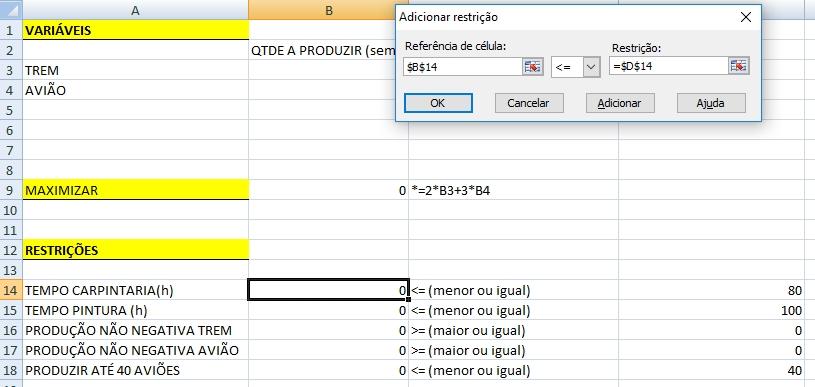
Na imagem acima, estou incluindo a restrição do tempo semanal da carpintaria, o campo Referência de célula representa a função da restrição de carpintaria, que está configurada na célula B14, selecionei a condição <= (menor ou igual) e no campo Restrição selecionei a célula D14, a qual expressa o total de horas da carpintaria na semana. Para incluir as demais restrições, clique no botão Adicionar até que, após incluir a última restrição, você clique no botão OK e finalize a inserção das restrições.
Após informar todas as restrições e clicar no botão OK, confira se todas estão corretas e clique no botão Resolver.
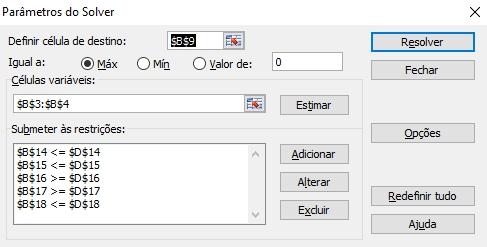
Após o Solver ter realizado todos os cálculos, ele apresentará (de acordo com o nosso exemplo) os seguintes resultados:
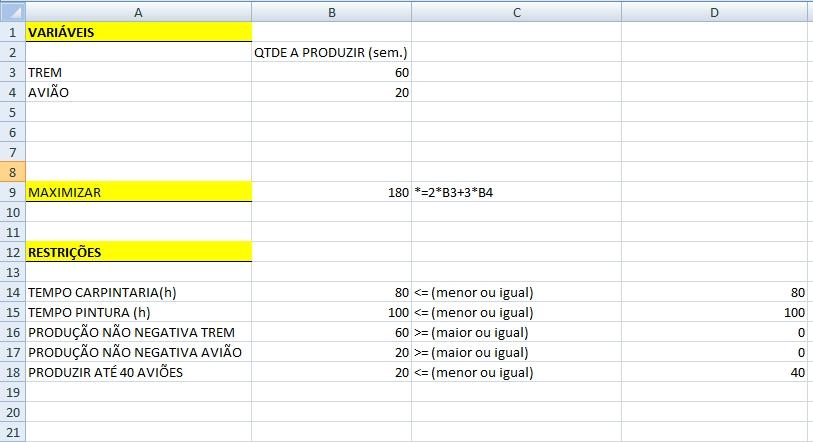
De acordo com os resultados apresentados, a quantidade a ser produzida/semana de trem será de 60 unidades e de aviões 20 unidades, com um lucro de R$ 180,00/semana. Ao verificarmos os resultados das restrições, vemos quais restringiram diretamente o resultado da equação.
Com essa produção, a quantidade de horas utilizadas da carpintaria (Célula B14) e da pintura (Célula B15) são exatamente iguais a capacidade de cada setor. Ou seja, as restrições que limitaram o crescimento do lucro da empresa é a “baixa” disponibilidade de seus recursos de produção, caso a empresa investisse em mais maquinário, poderia aumentar a sua produção bem como a oferta de seus produtos. As restrições de não negatividade das duas variáveis foram respeitadas (ambos produtos tiveram quantidade maior do que zero) e a restrição de produzir até 40 aviões por semana também foi respeitada, já que a quantidade sugerida pelo Solver foi de 20, menor do que as 40 unidades da restrição.
Outra função de como usar o Solver
O Solver ainda oferece uma ferramenta fantástica que é a análise de sensibilidade desses resultados, o qual consegue informar qual restrição precisa ser aumentada para potencializar ainda mais o resultado da função objetivo. No nosso caso, temos duas máquinas (carpintaria e pintura), a análise de sensibilidade informará qual dessas duas restrições trará mais lucro para o resultado da equação, caso a restrição seja aumentada (no caso da carpintaria, se ela tiver mais do que 80h/semana e da pintura ter mais do que 100h/semana). Mas, isso já é assunto para um outro artigo, que pretendo montar mais para a frente…







Participe! Deixe o seu comentário agora mesmo: